Calculator Demo
This demo shows how the VSFlexString control can be used to implement a mathematical expression evaluator. You can use this project as is, to allow users to enter expressions instead of numeric constants, or use it as a starting point for a more sophisticated evaluator with variables and custom functions.
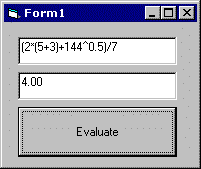
Here is how the final application will look:
Step 1: Create the Controls
Start a new Visual Basic project. Right-click on the Toolbox and select Components, then pick the VSFlexString control from the list. The VSFlexString icon will be added to the Visual Basic Toolbox. (If the control does not appear on the list, it hasn't been registered on your computer. In this case, click the Browse button and select the VSSTR8.OCX file to register it.)
Create a VSFlexString object on the form by clicking the icon on the Toolbox, then dropping it on the form. Also create two text boxes and a command button. Arrange the controls and resize the form so it looks like the picture above.
Click on the VSFlexString control and use the Visual Basic Property window to change its name to "fs".
Step 2: Evaluating Expressions
This project consists mainly of a single recursive function that uses the VSFlexString control to evaluate the expressions typed in the text box.
This function, which we will write later, needs to be called when the user clicks the button. Double-click the button and type the following into the event handler:
' Evaluate the expression in Text1 and show the result in Text2
Sub Command1_Click ()
Text2 = Format(Eval(Text1), "0.00")
End Sub
That leaves only the Eval function, which takes a string containing a mathematical expression as a parameter and returns a value. Here is the code:
Function Eval(ByVal s As String) As Double
Dim s1$, s2$, s3$
Dim v#
' get ready to parse
fs = Trim(s) ' set breakpoint on this line
' interpret sub-expressions enclosed in parentheses
fs.Pattern = "{.*}({[^()]*}){.*}"
If fs.MatchCount > 0 Then
s1 = fs.TagString(0) ' stuff to the left
s2 = fs.TagString(1) ' sub-expression
s3 = fs.TagString(2) ' stuff to the right
Debug.Print "match: "; s1; " #<(># "; s2; " #<)># "; s3
v = Eval(s2) ' evaluate sub-expression
Eval = Eval(s1 & Format(v) & s3)
Exit Function
End If
' add and subtract (high-priority operators)
fs.Pattern = "{.+}{[+-]}{.+}"
If fs.MatchCount > 0 Then
s1 = fs.TagString(0) ' operand 1
s2 = fs.TagString(2) ' operand 2
Debug.Print "match: "; s1; " #<+-># "; s2
Select Case fs.TagString(1)
Case "+": Eval = Eval(s1) + Eval(s2)
Case "-": Eval = Eval(s1) - Eval(s2)
End Select
Exit Function
End If
' multiply and divide (lower-priority operators)
fs.Pattern = "{.+}{[*/]}{.+}"
If fs.MatchCount > 0 Then
s1 = fs.TagString(0) ' operand 1
s2 = fs.TagString(2) ' operand 2
Debug.Print "match: "; s1; " #<*/># "; s2
Select Case fs.TagString(1)
Case "*": Eval = Eval(s1) * Eval(s2)
Case "/": Eval = Eval(s1) / Eval(s2)
End Select
Exit Function
End If
' power (lowest-priority operator)
fs.Pattern = "{.+}^{.+}"
If fs.MatchCount > 0 Then
s1 = fs.TagString(0) ' operand 1
s2 = fs.TagString(1) ' operand 2
Debug.Print "match: "; s1; "#<^>#"; s2
Eval = Eval(s1) ^ Eval(s2)
Exit Function
End If
' number (nothing else matched, so this should be a number)
fs.Pattern = "^-?[0-9]+\.?[0-9]*$"
If fs.MatchCount > 0 Then
Eval = Val(s)
Else
Debug.Print "Eval Error: "; fs: Beep
End If
End Function
This routine handles all basic operators taking into account their precedence (that is, power before division before sum). It also handles sub-expressions contained in parentheses.
The Eval function consists of a pattern that repeats itself. The VSFlexString is used to parse each expression into its components, according to operator priority rules, and Eval is called recursively to evaluate each component. This process continues until a number is found and evaluated using VB's built-in Val function.
The typical pattern has this format: "{.+}{[*/]}{.+}". The "{+.}" at the start and end of the pattern match runs of one or more characters. The "{[*/]}" matches an operator that separates the left and right parts of the expression.
Step 3: Trying it out
Press F5 to run the project and type an expression such as "(2*(5+3)+144^0.5)/7". Then click the command button and the result (4) will appear on the second text box. The debug window will show a trace of the Eval function. Here's a commented version of the output:
match: (2* #<(># 5+3 #<)># +144^0.5)/7 found sub-expression
match: 5 #<+-># 3 found +
match: #<(># 2*8+144^0.5 #<)># /7 found sub-expression
match: 2*8 #<+-># 144^0.5 found +
match: 144 #<^># 0.5 found ^
match: 2 #<*/># 8 found *
match: 28 #<*/># 7 found /
The trace shows the order in which matches were found and operations executed. You may want to place a breakpoint at the top of the Eval routine and see what happens after each match.
Step 4: Extending the Evaluator
As an exercise for the reader, try adding support for user-defined variables and functions such as Sin and Cos.